相机与图像
本章目标：
- 理解针孔模型、内参以及径向畸变参数
- 理解空间点如何投影到相机成像平面
- 掌握OpenCV图像存储与表达
- 掌握基本的摄像头标定方法
针孔模型
三维空间点与相机成像平面建模关系
$$\frac{Z}{f} = \frac{X}{X^,} = \frac{Y}{Y^,}$$
像素坐标系与成像平面间相差了一个缩放和原点的平移： $u = \alpha X^, + c_x, v=\beta Y^, + c_y$
将空间点与成像平面的公式代入，习惯性把Z左挪得到下式
.其中f单位为米，$\alpha，\beta$单位为像素每米，$f_x,f_y$单位为像素。K为相机内参，通常厂商会帮你标定给出，有时候需要自己确定或精细测量，就是摄像头标定。
为了更好成像效果，通常加入透镜，因此带来影响：1.透镜自身形状对光线传播的影响；2.机械组装透镜与成像平面不可能完全平行； 因此引入径向畸变和桶形畸变，它们引入的畸变均随着离中心的距离增加而增加。
纠正畸变过程：
- 1.将三维空间点投影到归一化图像平面，坐标为$[x,y]^T$
- 2.归一化平面的点进行经过5个参数进行径向和切向畸变校正：
$$x_{corrected} = x(1+k_1r^2+k_2r^4+k_3r^6) +2p_1xy +p_2(r^2+2x^2) $$
$$y_{corrected} = y(1+k_1r^2 +k_2r^4+k_3r^6)+p_1(r^2+2y^2)+2p_2xy$$ - 3.纠正后的点通过内参矩阵投影到像素平面，得到图像上正确的位置，生成新的纠正后的图像
$$u=f_xx_{corrected}+c_x$$
$$v=f_yy_{corrected}+c_y$$
总结单目相机成像过程：
- 1.首先世界坐标系下有一个固定点P，世界坐标为$P_w$
- 2.由于相机在运动，它运动由R,t或者变换矩阵T描述。P的相机坐标为$\hat{P_c} = RP_w +t$
- 3.此时$\hat{P_c}$仍由X，Y，Z三个量表示，需要投影到归一化平面Z=1上，得到P的归一化相机坐标：$P_c=[X/Z,Y/Z,1]^T$
- 4.最后将归一化坐标经过内参对应到像素坐标：$P_{uv}=KP_c$
个人思考：归一化坐标主要因为内参标定建立在一个参考平面，最general的就是建立在z=1米的参考平面上。这是由内参标定的参考平面决定的。
双目模型
水平放置左右相机在x轴上位移，有基线b。将左右成像中的像素匹配，求出视差图d。结合模型获得深度图。视差越大，距离越近。基线长则测得距离远，计算量和精度问题，且需要图像纹理丰富变化。
RGBD相机
红外结构光：Intel RealSense 以及面TOF相机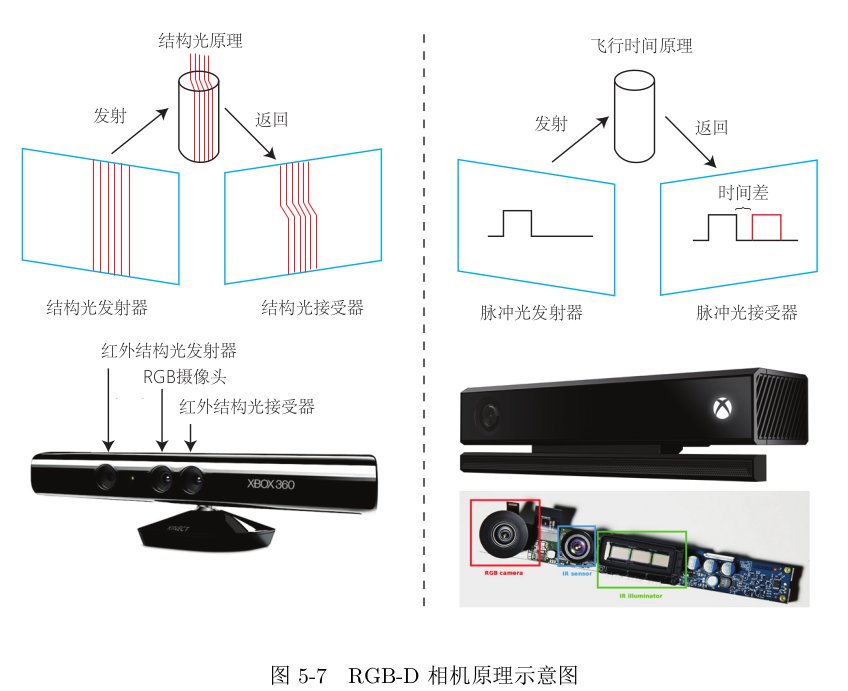
非线性优化
目标：
- 理解最小二乘含义和处理方式
- 理解高斯牛顿和LM下降
- 学习Ceres和g2o用法
EKF不考虑历史，只关心当前时刻的状态估计；而非线性优化使用了所有时刻采集的数据进行状态估计。
贝叶斯法则，x为相机位姿，z为路标在图像上的像素位置。进一步，假设观测路标与位姿满足高斯分布，用最小化负对数可便利地求MLE。
直观而言，由于观测和运动方程噪声存在，当把估计的轨迹与地图代入SLAM模型时，方程组不会完美成立。因此对位姿的估计值进行微调，使得总体误差下降，当降到极小值即优化完毕。这就是典型的非线性优化过程。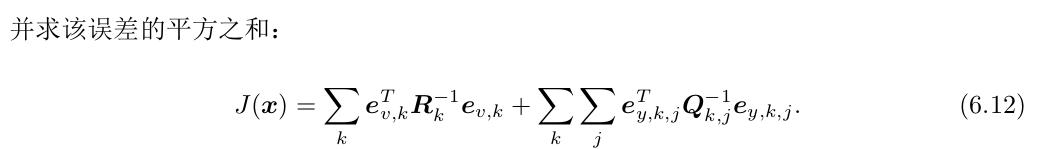
SLAM的最小二乘具有特定结构：
- 目标函数由许多个误差的平方和组成，每个误差项只与上一时刻相关，小规模的约束
- 总体误差的增量方程具有一定的稀疏性
- 使用李代数时为无约束的最小二乘问题，若旋转矩阵引入额外约束而复杂
- 可用其他范数构建优化问题
最小二乘问题
$$min_x \frac{1}{2} ||f(x)||_2^2$$
若f(x)形式简单，可用解析解对f求x上的导数为0的极值点，再回代比较；但是SLAM的李代数导数形式时非线性方程，所以要用计算机中迭代的过程逼近：
- 1.给定初始值$x_0$
- 2.对第k次迭代寻找增量$\Delta x_k$使目标函数极小
- 3.若$\Delta x_k$足够小（位姿误差），则停止
- 4.否则$x_(k+1) = x_k + \Delta x_k$,继续2.
只需要找到local minimum,主要问题变为如何确定增量$\Delta x_k$
导数展开，只取一阶导雅可比为0，最速下降法，但过于贪心容易锯齿反而增加迭代
只取二阶导为0则引入海塞矩阵，问题规模较大使二阶导系数H不容易计算。如此一来，便促使研究引入更为实用的高斯牛顿法和LM列文伯格-马夸尔特方法。
高斯牛顿下降法 line search
不同于对x求导，这里对$\Delta x$求导
如此GN用$J^TJ$作为牛顿法中二阶Hessian矩阵的近似，优化了计算。但要求保证近似H可逆正定。但实际中可能出现为奇异矩阵或者病态，此时增量稳定性不佳导致算法不收敛。虽然GN有不少问题，但很多实用方法是从这个思想优化延伸的。
LM阻尼牛顿法
GN采用近似二阶泰勒只能在展开点附近有较好近似效果，因此对$\Delta x$添加信赖域区域，使它不能过大而不准确，这类方法也叫信赖区域法(Trust Region Method)。
如何确定可用的信赖区域？ 比较近似模型跟实际函数之间的差异
工作流程：
LM求解过程一定程度上避免线性方程组的系数矩阵非奇异和病态问题，提供更稳定准确的增量$\Delta x$
小结
数值优化和最优化是解决实际问题中的基本数学工具，可以感兴趣多了解。
非线性优化的迭代求解方案均需要提供一个良好的初始值，不同的初始值导致不同的计算即过，这是通病。因此如何提供科学的初始值以及算法阈值是很重要的事情！
对大矩阵求逆可以用QR、Cholesky分解；对大的稀疏矩阵也有相关消元分解，求增量的方法具体可了解矩阵论。
Ceres为谷歌开源库，针对非线性优化问题，主要用法：
- 定义cost function模型。书写类，定义带模板参数的()运算符，使成为拟函数Functor,从而像调用函数一样使用如类a
() - 调用AddResidualBlock将采集数据的误差项添加到目标函数：通常使用Ceres自动求导
- 设定好后调用solve函数求解
g2o进一步把SLAM优化问题用图论描述，成为图优化问题。节点表示优化变量，边为误差项。
使用流程：
1.顶点的更新函数：位姿更新需要重新定义左乘或者右乘的更新
2.顶点重置以及边的误差计算，获得所有边连接顶点的估计值
3.读写结果
课后习题总结：
1.矩阵A正定，则rank(A) = n, 可求逆。欠定则有多组解，超定则无解，有最小二乘解。
2.最速法过于贪心二迭代次数多，牛顿法需计算海塞矩阵，二者均不实用；SLAM常用GN，LM和Dog-Leg狗腿法：高斯牛顿简单高效，但病态矩阵时容易发散；LM是可信域法，略满于GN但正定性强，不易发散；狗腿与LM类似，为解决GN近似计算Hessian不准确而提出的。一般的优化库还包括Nlopt,slam++等。
3.A不满秩时，近似的H也半正定，越不正定越接近0矩阵，求逆误差越大，因此$\Delta x$越不可靠
4.狗腿法具体看https://blog.csdn.net/qq_35590091/article/details/94628887